Perimeter & Area are two very important and fundamental math topics.
These topics help you quantify physical space and provide the foundation for more advanced math issues found in algebra, calculus, and trigonometry.
Onsego GED Prep
Online GED Classes
Lessons Simply Explained | Practice Tests | Add-ons
Preview Onsego Now
Click here for the next lesson
Video Transcription
Perimeters are measurements of the distance around shapes, and Areas give us an idea of the surface a shape covers.
The knowledge of perimeter and area is applied in a practical way by lots of people on a day-to-day basis. Engineers, architects, and graphic designers use it every day. This is math that’s so much needed by individuals in general everywhere.
Understanding how much space we’ve got and learning how we can fit shapes together in an exact way will be helpful when painting a room, buying a home, remodeling a kitchen, or building a deck.
Online GED Classes
Pass Your GED with ease
It doesn’t matter when you left school.
Instant Preview
Perimeter
The perimeter of a 2-dimensional shape is the distance around that shape. Think of wrapping some string around a triangle. Then, the length of that string would be the triangle’s perimeter. When you walk around the outside of a park, you’ll be walking the distance of the perimeter of that park.
Some people find it useful to think of a “peRIMeter” as an object’s edge is its rim. Well, peRIMeter has the word “rim” in it.
Now, if your shape is a polygon, you can add up all the polygon’s lengths of its sides to find its perimeter. Be careful: make sure that you measure all the lengths in the same units of measure. You measure the perimeter in linear units, and these are 1-dimensional. The units of measure examples for length are feet, inches, or centimeters.
Example
The problem: What is the perimeter of this figure? The measurements given are inches.
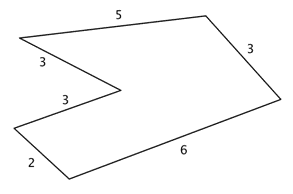
Well, the perimeter (P) is: 5 + 3 + 6 + 2 + 3 + 3
All sides are measured in inches, so just add all the lengths of the six (6) sides to get your perimeter.
Remember that you must include units.
So the answer is P = 22 inches.
That’s meaning that a tightly wrapped string that runs the distance around the entire polygon will measure a length of 22 inches.
Another example
The problem: What is the perimeter of a triangle that has sides that measure 6 cm, 8 cm, and 12 cm?
The perimeter (P) is: 6 + 8 + 12
As all of the triangle’s sides are measured in centimeters, simply add all the lengths of the three sides to get our perimeter.
The answer is: P = 26 centimeters.
Sometimes, we must use what we know about a polygon to find our perimeter. Let’s take a look at the rectangle in the following example.
Example
The problem: A rectangle has a width of 3 centimeters and a length of 8 centimeters. Find its perimeter.
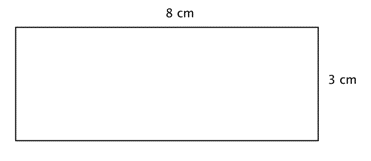
P = 3 + 3 + 8 + 8
Because this is a rectangle, opposite sides have exactly the same lengths, 8 cm. and 3 cm. So add up all lengths of the four sides to find our perimeter.
The answer is: P = 22 cm.
Did you see that the perimeter (P) of a rectangle always includes two pairs of equal-length sides? In the example above, you might have also written: perimeter (P) = 2(3) + 2(8) = 6 + 16 = 22 cm. The formula for measuring the perimeter of rectangles is often written as follows: P = 2l + 2w. Here, l is the rectangle’s length, and w is the rectangle’s width.
Last Updated on September 11, 2024.